Data assimilation is the process by which observations are incorporated into the numerical weather model state. Assumi ng weather system under study is a random process, the solution of the data assimilation problem is the probability density function (PDF) of the system conditioned upon observations.

In this work, the data assimilation system is Gridpoint Statistical Interpolation (GSI). The GSI capability to be evaluated in this work is the hybrid 4D EnVar, in comparison with GSI 3DVar and hybrid 3D EnVar.

Variational (Var) data assimilation (DA)

A variational method using static (climatology) background error covariances.

• Cost Function:

Analysis is achieved by finding the minimum x of the cost function, J(x).

Assuming background errors and observations are Gaussian, 3DVar and 4DVar solutions are the unbiased minimum variance estimates<=>the maximum likelihood estimates.

• X(Xb): analysis (background) state vector

• y: observation vector

• B (R): background (observation) error covariance

• H: observation (forward) operator

3D Hybrid Ensemble-Variational (EnVar) DA

A variational method using a combination of static and ensemble covariances - alleviate ensemble localization issues/allow for more efficient error estimation with necessarily small ensembles

• Cost Function:

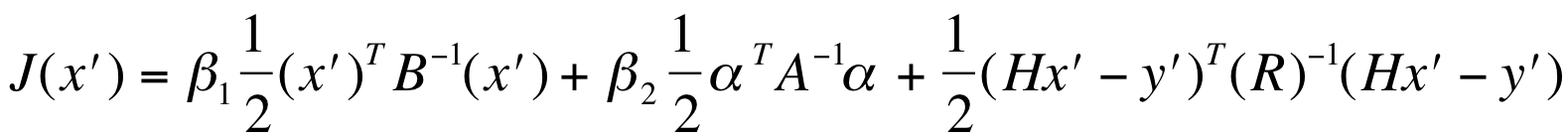
Analysis is achieved by finding the minimum x of the cost function, J(x).

• x': Analysis increment (Xa-Xb)

• y': innovations, y-H(x)

• β1 (β2): weighting functions, specifying the wighting of the static and ensemble background errors.

• α: extended control variable

• A: Correlation matrix

4D Hybrid Ensemble-Variational (EnVar) DA

Similar to 3DEnVar, a variational method using a combination of static and ensemble covariances. However, in 3DEnVar enemble perturbations do not vary in window but in 4DEnVar ensemble perturbations vary in time within window.

• Cost Function:

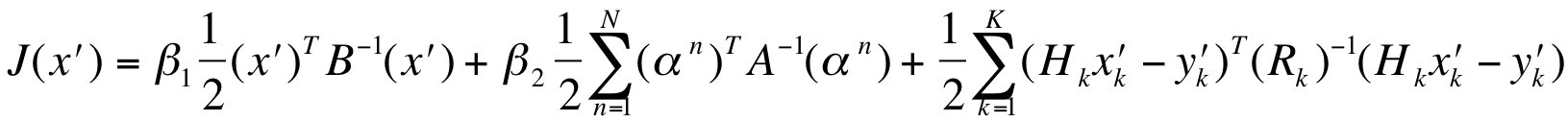
Analysis is achieved by finding the minimum x of the cost function, J(x).

• x': Analysis increment (Xa-Xb)

• y': innovations, y-H(x)

• β1 (β2): weighting functions, specifying the wighting of the static and ensemble background errors.

• α: extended control variable

• A: Correlation matrix

• n: n-th ensemble member

• k: k-th time bins