Hydromet Testbed Model Evaluation

HMT 2010 Field Campaign - Spatial Methods
Spatial Verification Methods
MODE summary metrics
The Method for Object-based Diagnostic Evaluation (MODE) identifies and matches spatial objects in the forecast and observed fields. A convolution radius (r) and a precipitation/reflectivity threshold (t) are used to identify objects; different combinations of these parameters lead to objects with different characteristics, and can be used to evaluate forecasts as a function of threshold and scale.
In the object matching and merging[1] process, all possible pairs of forecast and observed objects are assigned a total “interest” value. This value is formulated from the weighted sum of specific interest values that are associated with differences in particular attributes between the forecast and observed objects. According to the current weighting scheme, the total interest value is large when objects are located close to each other and are about the same size, and is smaller for pairs of objects that are further apart and have different sizes. Note that users can specify other components of interest, and their relative weights, in the configuration file for running MODE, according to what is most relevant for their particular application.
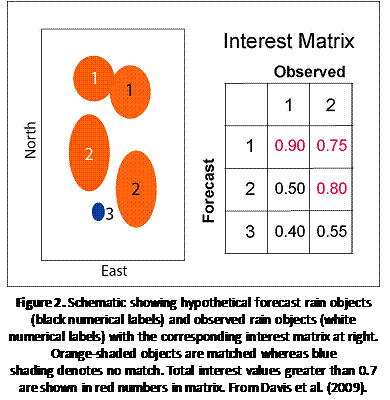
Figure 2 illustrates a scenario in which three forecast objects and two observed objects have been identified in the two fields. The total interest values for all of the pairs of forecast and observed objects are shown in the associated table. In previous work an interest threshold of 0.70 has been found to be a reasonable indicator of a good match. Thus, in this case, forecast object 1 is a good match with both observed objects 1 and 2, and forecast object 3 matches well with observed object 2. Forecast object 3 does not match well with either of the observed objects, mostly because of its small size. Because both forecast objects 1 and 2 match observed object 2, and forecast object 1 also matches observed object 1, these objects form a matched “cluster” in the forecast and observed fields.
Some of the forecast attributes that are (or can be considered) in determining matches between forecast and observed objects include object size, distribution of intensity values, orientation angle, and location. Comparisons of these attributes, along with the total interest values, also can be used to help measure the quality of the forecast performance. Some of the measures that can be used to summarize performance using MODE are described in the following subsections.
Median of Maximum Interest (MMI)
This measure is computed using the total interest values for all of the pairs of objects. It considers the maximum total interest values associated with each forecast object and each observed object. From this set, the median value is computed and is the MMI.
Example: Forecast and observed objects in Fig. 2
Maximum interest values for all of the forecast and observed objects are as follows:
For forecast object 1, the maximum total interest is 0.90.
For forecast object 2, the maximum total interest is 0.80.
For forecast object 3, the maximum total interest is 0.55.
For observed object 1, the maximum total interest is 0.90.
For observed object 2, the maximum total interest is 0.80.
The median of those 5 numbers is 0.80, so MMI = 0.80.
This number can be small because no objects match well, or because there are many extra objects that don’t match well.
Larger MMI values imply a better match between forecast and observed objects.
Area-Weighted CSI
Area Weighted Critical Success Index (AWCSI)
AWCSI = [(hit area weight) * #hits ] / [(hit area weight * # hits) + (miss area weight * # misses) + (false alarm area weight * # false alarms) ]
Where each area weight is the ratio of size of the (hit, miss, or false alarm) objects to the total area of all objects and # hits = number of matched objects; # misses = # unmatched observed objects; and # false alarms = # unmatched forecast objects.
Answers the question: How well did the forecast "yes" objects correspond to the observed "yes" objects?
Range: 0 to 1, 0 indicates no skill. Perfect score: 1.
Characteristics: Measures the area-weighted fraction of observed and/or forecast events that were correctly predicted. It can be thought of as the accuracy when correct negatives have been removed from consideration. That is, CSI is only concerned with forecasts that important (i.e., assuming that the correct rejections are not important). Sensitive to hits; penalizes both misses and false alarms. Does not distinguish the source of forecast error.
In a grid-based CSI, each gridpoint that is counted in computing the CSI represents an area with the same size, but with MODE objects, the various objects can have a wide variety of sizes. Thus, area weighting makes sense.
Mean Intersection over Area
Ratio of intersection area to union area (unitless). Ranges from zero to one: One is perfect, smaller implies less overlap. This measure is the mean for all clusters of objects with interest values greater than 0.7.
Area Ratio
Ratio of the areas of two objects defined as the lesser of the forecast area divided by the observation area or its reciprocal (unitless). The ideal value is 1, since this means that the forecast and observed objects are exactly the same size. Smaller implies that the forecast was either too small or too large. This measure is the mean for all clusters of objects with interest values greater than 0.7.
Centroid Distance
Distance between two objects centroids (in grid units). Smaller is better, since this means the objects are closer. This measure is the mean for all clusters of objects with interest values greater than 0.7.
Angle Difference
Difference between the axis angles of two objects (in degrees). This is only meaningful if objects seem to be more linear than circular, e.g. lines of thunderstorms. When they are linear, this measure tells you how well the angle of the forecast line matches the angle of the observed line. Smaller differences are better. This measure is the mean for all clusters of objects with interest values greater than 0.7.
Intensity with confidence intervals
10th, 25th, 50th, 75th, and 90th percentiles of intensity of the filtered field within the object (various units). This tells you the distribution of values within an object (think of this as the numeric equivalent of a boxplot). There are no ideal values. However, if you compare the distribution of values within a forecast object and an observed object, you would like them to match up. For example, check to see how close the median and 90th percentile values are. This will tell you if the forecast is too intense or too weak. This measure is the mean for all clusters of objects with interest values greater than 0.7.
Learn more about MET and MODE.
View Feb 2009 MET Tutorial Presentation on how objects are defined in MODE.
View Feb2009 MET Tutorial Presentation on how matching and merging of objects is done in MODE.
Interest Map settings for Matching and Merging for this Experiment:
centroid_dist_if = {
( 0.0, 1.0 )
( 40.0/grid_res, 1.0 )
( 400.0/grid_res, 0.0 )
};
boundary_dist_if = {
( 0.0, 1.0 )
( 160.0/grid_res, 1.0 )
( 800.0/grid_res, 0.0 )
};
convex_hull_dist_if = {
( 0.0, 1.0 )
( 160.0/grid_res, 1.0 )
( 400.0/grid_res, 0.0 )
};
angle_diff_if = {
( 0.0, 1.0 )
( 30.0, 1.0 )
( 90.0, 0.0 )
};
corner = 0.8;
ratio_if = {
( 0.0, 0.0 )
( corner, 1.0 )
( 1.0, 1.0 )
};
area_ratio_if(x) = ratio_if(x);
int_area_ratio_if = {
( 0.00, 0.00 )
( 0.10, 0.50 )
( 0.25, 1.00 )
( 1.00, 1.00 )
};
complexity_ratio_if(x) = ratio_if(x);
intensity_ratio_if(x) = ratio_if(x);
