GFS Operational Physics Documentation  Revision: 81451
Precipitation (snow or rain) Production
Grid-scale Condensation, Evaporation and Precipitation

This subroutine computes the conversion from condensation to precipitation (snow or rain) or evaporation of rain. More...

Detailed Description

This subroutine computes the conversion from condensation to precipitation (snow or rain) or evaporation of rain.

The parameterization of precipitation is required in order to remove water from the atmosphere and transport it to the ground. In the scheme discussed here, simplifications in the precipitation parameterization are used due to computational limitations required by operational NWP models. First, consideration of particle size and shape can be avoided by using the bulk parameterization method introduced by Kessler (1969) [32]. Second, only two types of precipitation, rain and snow, are considered in this scheme. Third, only the most important microphysical processes associated with the formation of rain and snow are included. Figure 2 presents the microphysical processes considered in the precipitation parameterization.

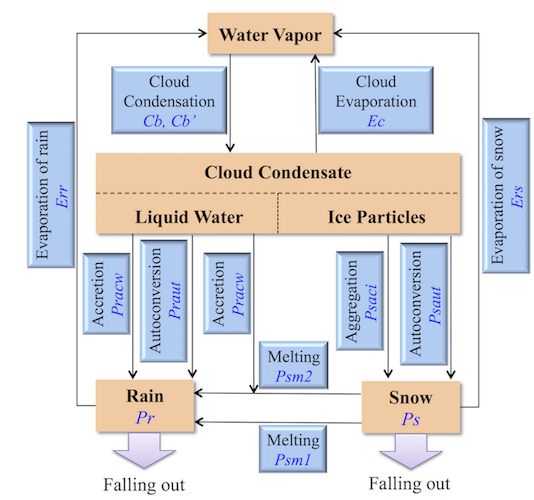
precpd-micop.png

"Figure 2: Microphysical processes simulated in the precipitation scheme " width=5cm Basically, there are four types of microphysical processes considered here:

The following two equations can be used to calculate the precipitation rates of rain and snow at each module level:

\[ P_{r}(\eta)=\frac{p_{s}-p_{t}}{g\eta_{s}}\int_{\eta}^{\eta_{t}}(P_{raut}+P_{racw}+P_{sacw}+P_{sm1}+P_{sm2}-E_{rr})d\eta \]

and

\[ P_{s}(\eta)=\frac{p_{s}-p_{t}}{g\eta_{s}}\int_{\eta}^{\eta_{t}}(P_{saut}+P_{saci}-P_{sm1}-P_{sm2}-E_{rs})d\eta \]

where \(p_{s}\) and \(p_{t}\) are the surface pressure and the pressure at the top of model domain, respectively, and \(g\) is gravity. The implementation of the precipitation scheme also includes a simplified procedure of computing \(P_{r}\) and \(P_{s}\) (Zhao and Carr(1997) [58]).

Collaboration diagram for Precipitation (snow or rain) Production:
subroutine precpd (im, ix, km, dt, del, prsl, q, cwm, t, rn, sr , rainp, u00k, psautco, prautco, evpco, wminco , lprnt, jpr)
 

Function/Subroutine Documentation

subroutine precpd ( integer  im,
integer  ix,
integer  km,
real (kind=kind_phys)  dt,
real (kind=kind_phys), dimension(ix,km)  del,
real (kind=kind_phys), dimension(ix,km)  prsl,
real (kind=kind_phys), dimension(ix,km)  q,
real (kind=kind_phys), dimension(ix,km)  cwm,
real (kind=kind_phys), dimension(ix,km)  t,
real (kind=kind_phys), dimension(im)  rn,
real (kind=kind_phys), dimension(im)  sr,
real (kind=kind_phys), dimension(im,km)  rainp,
real (kind=kind_phys), dimension(im,km)  u00k,
real (kind=kind_phys), dimension(im)  psautco,
real (kind=kind_phys), dimension(im)  prautco,
real (kind=kind_phys)  evpco,
real (kind=kind_phys), dimension(2)  wminco,
logical  lprnt,
integer  jpr 
)
Parameters
[in]imhorizontal number of used pts
[in]ixhorizontal dimension
[in]kmvertical layer dimension
[in]dttime step in seconds
[in]delpressure layer thickness (bottom to top)
[in]prslpressure values for model layers (bottom to top)
[in,out]qspecific humidity (updated in the code)
[in,out]cwmcondensate mixing ratio (updated in the code)
[in,out]ttemperature (updated in the code)
[out]rnprecipitation over one time-step dt (m/dt)
[out]sr"snow ratio", ratio of snow to total precipitation
[out]rainprainwater path
[in]u00kthe critical value of relative humidity for large-scale condensation
[in]psautcoauto conversion coeff from ice to snow
= 4.0E-4; defined in module_MP_GFS.F90
[in]prautcoauto conversion coeff from cloud to rain
= 1.0E-4; defined in module_MP_GFS.F90
[in]evpcocoeff for evaporation of largescale rain
= 2.0E-5; defined in module_MP_GFS.F90
[in]wmincocoeff for water and ice minimum threshold to conversion from condensate to precipitation
= \1.0E-5, 1.0E-5\; defined in module_MP_GFS.F90
[in]lprntlogical print flag
[in]jprcheck print point for debugging

General Algorithm

  1. Select columns where rain can be produced, where

    \[ cwm > \min (wmin, wmini) \]

    where the cloud water and ice conversion threshold:

    \[ wmin=wminco(1)\times prsl\times 10^{-5} \]

    \[ wmini=wminco(2)\times prsl\times 10^{-5} \]

  2. Compute ice-water identification number IW (see algorithm in Grid-Scale Condensation and Evaporation of Cloud).
  3. Calculate cloud fraction \(b\) (see algorithm in Grid-Scale Condensation and Evaporation of Cloud)
  4. Precipitation production by auto conversion and accretion
    • The autoconversion of cloud ice to snow ( \(P_{saut}\)) is simulated using the equation from Lin et al. (1983) [35]

      \[ P_{saut}=a_{1}(cwm-wmini) \]

      Since snow production in this process is caused by the increase in size of cloud ice particles due to depositional growth and aggregation of small ice particles, \(P_{saut}\) is a function of temperature as determined by coefficient \(a_{1}\), given by

      \[ a_{1}=psautco \times dt \times exp\left[ 0.025\left(T-273.15\right)\right] \]

    • The accretion of cloud ice by snow ( \(P_{saci}\)) in the regions where cloud ice exists is simulated by

      \[ P_{saci}=C_{s}cwm P_{s} \]

      where \(P_{s}\) is the precipitation rate of snow. The collection coefficient \(C_{s}\) is a function of temperature since the open structures of ice crystals at relative warm temperatures are more likely to stick, given a collision, than crystals of other shapes (Rogers 1979 [47]). Above the freezing level, \(C_{s}\) is expressed by

      \[ C_{s}=c_{1}exp\left[ 0.025\left(T-273.15\right)\right] \]

      where \(c_{1}=1.25\times 10^{-3} m^{2}kg^{-1}s^{-1}\) are used. \(C_{s}\) is set to zero below the freezing level.
    • Following Sundqvist et al. (1989) [51], the autoconversion of cloud water to rain ( \(P_{raut}\)) can be parameterized from the cloud water mixing ratio \(m\) and cloud coverage \(b\), that is,

      \[ P_{raut}=(prautco \times dt )\times (cwm-wmin)\left\{1-exp[-(\frac{cwm-wmin}{m_{r}b})^{2}]\right\} \]

      where \(m_{r}\) is \(3.0\times 10^{-4}\).
    • Calculate the accretion of cloud water by rain \(P_{racw}\), can be expressed using the cloud mixing ratio \(cwm\) and rainfall rate \(P_{r}\):

      \[ P_{saci}=C_{s}cwmP_{r} \]

      where \(C_{r}=5.0\times10^{-4}m^{2}kg^{-1}s{-1}\) is the collection coeffiecient. Note that this process is not included in current operational physcics.
  5. Evaporation of precipitation ( \(E_{rr}\) and \(E_{rs}\))
    Evaporation of precipitation is an important process that moistens the layers below cloud base. Through this process, some of the precipitating water is evaporated back to the atmosphere and the precipitation efficiency is reduced.
    • Evaporation of rain is calculated using the equation (Sundqvist 1988 [52]):

      \[ E_{rr}= evpco \times (u-f)(P_{r})^{\beta} \]

      where \(u\) is u00k, \(f\) is the relative humidity. \(\beta = 0.5\) are empirical parameter.
    • Evaporation of snow is calculated using the equation:

      \[ E_{rs}=[C_{rs1}+C_{rs2}(T-273.15)](\frac{u-f}{u})P_{s} \]

      where \(C_{rs1}=5\times 10^{-6}m^{2}kg^{-1}s^{-1}\) and \(C_{rs2}=6.67\times 10^{-10}m^{2}kg^{-1}K^{-1}s^{-1}\). The evaporation of melting snow below the freezing level is ignored in this scheme because of the difficulty in the latent heat treatment since the surface of a melting snowflake is usually covered by a thin layer of liquid water.
  6. Melting of snow ( \(P_{sm1}\) and \(P_{sm2}\))
    In this scheme, we allow snow melting to take place in certain temperature regions below the freezing level in two ways. In both cases, the melted snow is assumed to become raindrops.
    • One is the continuous melting of snow due to the increase in temperature as it falls down through the freezing level. This process is parameterized as a function of temperature and snow precipitation rate, that is,

      \[ P_{sm1}=C_{sm}(T-273.15)^{2}P_{s} \]

      where \(C_{sm}=5\times 10^{-8}m^{2}kg^{-1}K^{-2}s^{-1}\) cause the falling snow to melt almost completely before it reaches the \(T=278.15 K\) level.
    • Another is the immediate melting of melting snow by collection of the cloud water below the freezing level. In order to calculate the melting rate, the collection rate of cloud water by melting snow is computed first. Similar to the collection of cloud water by rain, the collection of cloud water by melting snow can be parameterized to be proportional to the cloud water mixing ratio \(m\) and the precipitation rate of snow \(P_{s}\):

      \[ P_{sacw}=C_{r}cwmP_{s} \]

      where \(C_{r}\) is the collection coefficient, \(C_{r}=5.0\times 10^{-4}m^{2}kg^{-1}s^{-1}\) . The melting rate of snow then can be computed from

      \[ P_{sm2}=C_{ws}P_{sacw} \]

      where \(C_{ws}=0.025\).
    • Update t and q.

      \[ t=t-\frac{L}{C_{p}}(E_{rr}+E_{rs}+P_{sm1})\times dt \]

      \[ q=q+(E_{rr}+E_{rs})\times dt \]

  7. Compute precipitation at surface ( \(rn\))and determine fraction of frozen precipitation ( \(sr\)).

    \[ rn= (P_{r}(\eta_{sfc})+P_{s}(\eta_{sfc}))/10^3 \]

    \[ sr=\frac{P_{s}(\eta_{sfc})}{P_{s}(\eta_{sfc})+P_{r}(\eta_{sfc})} \]

Definition at line 81 of file precpd.f.

References physcons::con_cp, physcons::con_g, physcons::con_hfus, physcons::con_hvap, and physcons::con_ttp.

Referenced by gbphys().

Here is the caller graph for this function: